Appendix A

11

In this proposal the quantized space-time coordinates and 4-momentum (translation) operators are expressed as linear differential operators on a background space. The values of the commutation relations, seen in eq. () of appendix A.6 for these operators, give the generators of the Lorentz group.

12

Incidentally this also solves a very basic problem of quantum gravity, called quantum foam. A sequential magnification of a region of space enables vacuum fluctuations of the gravitational field (allowed by the uncertainty relation) to become evermore violent, in effect ripping up space and time. Hence the notion of a smallest length scale shields reality from this destructive quantum foam.

13

String theory offers two different but related operational definitions of distance. So-called T duality hints at the involved mechanisms. Two string theories are T-dual if one theory compactified on a space with large radius 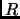$R$ is equivalent to the second theory compactified on a space with radius 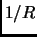$1/R$.^B.7 E.g. 10-dimensional IIA (HS) theory compactified onto a circle is T-dual to 10-dimensional IIB (HE) theory compactified onto a circle. In these scenarios there exists two kinds of string excitations. So-called Kaluza-Klein states (which are not special to string theory and are related to the compact space) have energies 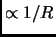$\propto 1/R$. Winding-mode excitations (which are special to string theory and can be visualized as strings wrapped around compact dimension) have energies 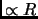$\propto R$. The result is that at large distance scales Kaluza-Klein modes are light (i.e. associated with small energies), whereas the winding modes are heavy. At the Planck scale where 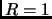$R =1$ per definition, both modes have comparable mass. Below the Planck scale the winding modes are the light ones. Basically these two modes could be employed as probes to measure distances (as multiples of the Planck length) with inversely related results. I.e. Kaluza-Klein modes measure a length 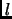$l$ while the winding modes measure 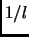$1/l$ because the higher the energy the smaller the probed distance ( 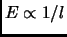$E \propto 1/l$). It is a technical difficulty to measure distances with heavy probes. This is why the two possible notions of distance have never been encountered by science, meaning that light probes are the natural choice. Hence a pragmatic operational definition of distance would always require the light modes to be employed. As a result Kaluza-Klein modes are used to probe distances greater than the Planck length (measuring 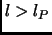$l > l_{P}$) and winding modes are used to probe distances smaller than the Planck length (however measuring 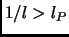$1/l > l_{P}$). So the question of what is smaller than the Planck length looses its meaning giving 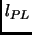$l_{PL}$ the significance of being the smallest `quantum' of distance.

14

If this ontological possibility is in fact true and the underlying level of the physical reality is finite and bounded then it raises the interesting question of why our minds can so easily conceive the notion of infinity through the simple question: what lies beyond the boundary?, in effect giving rise to the idea of an infinite series of progression. Mathematics, being a product of intellect also intimately uses and relies the notions of infinity.

A consequence of the reality of this fact would be that our universe is positively curved. Even the slightest value of such a curvature yields a closed and finite universe, just as the 2-dimensional surface of a sphere is finite and bounded.

15

The possibility of particles being black holes has already been examined by [#!Mo62!#] and [#!Ma67!#], over thirty years ago.

16

There exists another interesting proposal also related to the concept of information, based on information theory. The core idea is the notion of Fisher information, named after the Cambridge statistician Fisher in 1925. The amount of Fisher information, 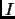$I$, of a system quantitatively gives the possible measure of information which can be extracted from a system under surveillance. Another statistical quantity is the total information contained in the same system, 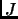$J$. Frieden puts 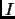$I$ into relation with 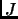$J$ and requires 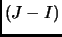$(J-I)$ to be minimal, i.e. the retrieved information maximal. This is taken as the physical principle -- somewhat reflecting the extremal principle of least action -- and is used to derive the Lagrangians (and hence the corresponding Euler-Lagrange equations) of a wide range of physics: Maxwell's equations of electromagnetism, the Klein-Gordon and Dirac equations of relativistic QM, the Einstein field equations of GR and the Wheeler-de Witt equations of quantum gravity; [#!Fr98!#]. Hence physical laws are the result of the maximal information being obtained from reality, or more succinctly: physical laws are the best information one can ever extract from nature. This would intimately relate the act of observation and the observer with reality itself (this problem will re-appear in appendix A.8). Consult [#!NS99iii!#]. Some other applications of Fisher information: in inflation, [#!GL00!#]; concerning times arrow, [#!FR98!#]; and in QM [#!Ha99!#], [#!Re99!#], [#!BG00!#], [#!Petz01!#].

Interestingly and more rigorously, there is a geometric approach to statistics also employing Fisher information, called information geometry. Consult appendix B.

17

It is somewhat intriguing to note that Smolin also reaches a similar conclusion within the context of string/M-theory: `according to which [the holographic principle], the world is constructed out of nothing but the flow of information'; front flap of [#!Sm00!#].

18

This notion of an information based reality seems to be fascinating many popular science writer, e.g. [#!Si00!#] and [#!Da00!#].

19

On more scientific ground, Fredkin is known for the development of a new logic gate: a variant to the classical binary logic switches AND, OR and NOT found in every digital computer. The Fredkin gate is reversible (i.e. no information is lost in the processing, unlike an AND gate, for example) and it is universal (meaning it can be used to construct any possible binary logic circuit); [#!Br00!#].

20

Also Descartes could only conclude with total certainty that the only thing which withstood his critical thinking and doubting was the reality of his thoughts, which in turn concluded his existence.