Chapter 4

4

It is interesting to note that GR and the SM are in fact united at a mathematical level. As seen in notes [#!ch1sym2!#] and [#!ch2au2!#] the symmetry concept gives rise to both gauge theories and GR. The connection is as follows. Gauge theories are mathematically expressed within the framework of group theory and for GR the corresponding mathematical formalism is differential geometry. There is an intimate mathematical connection (unification) between group theory and differential geometry.

The unifying attempts of string/M-theory have added a third mathematical member to the above topics: topology. Topology, differential geometry and group theory are in fact all part of what mathematicians understand under the general term of geometry. Thus the ideas expressed in note [#!ch1hm4!#] can be stated more accurately: geometry seems to be the most ideal (only?) language/formalism/intellectual concept in which the workings of reality can be expressed and future events deduced. It is also an interesting fact that the founders of of geometry, among them Euler, Gauss, Jacobi, Riemann and Poincaré, were profoundly interested in `natural philosophy', i.e. in understanding the eternal workings of nature in the lines of thought first proposed by the Greek philosophers Socrates, Plato and Aristotle.

For references and further ideas consult appendix B.

5

As mentioned in note [#!ch2au3!#] string/M-theory, although actually unifying all forces and matter, is also not able to give any conclusive answers. So in fact a further understanding of nature could actually also aid string/M-theory in reaching the everyday world we inhabit.

6

In essence Thomas von Aquin manages to synthesize Christian faith with reason and knowledge, i.e. philosophy and theology with science, by carefully weaving the rational ideas of Aristotle -- probably the first scientist in recorded history, using logic and starting metaphysics, which itself unites ontology, theology, psychology and cosmology -- on the nature of reality with the Christian belief of the spiritual world into one tapestry.

7

In 1930 Gödel rocked the foundations of mathematics. Up to then mathematics was believed as being a totally consistent and logical formal structure. However, Gödel proved that in every consistent non-contradictory system of mathematical axioms leading to elementary arithmetics of whole numbers, there exist statements which, although resting on the axioms, can not be proved or disproved in the system. He even showed that the very notion of the non-contradictoriness of the axioms is such a statement meaning that there is no constructive procedure which will prove an axiomatic theory to be consistent; [#!De88!#].

Russell, a mathematician, philosopher and (literature) Nobel laureate, was also interested in the logical foundations of mathematics, namely in sets and their relationships. In 1901 he encountered a paradox. 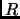$R$ is said to be a Russell set if it does not contain itself as a member. Hence if 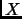$X$ is not a Russell set then 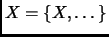$X =\{ X, \dots\}$. However, the set of all Russell sets, called 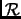$\mathcal R$, is neither a Russell set nor a non-Russell set because if 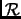$\mathcal R$ is a Rusell set, then per definition it is not a Rusell set. The argument works vice versa; [#!Du94!#]. Interestingly this is reminiscent of the old QM paradox of the wave-particle duality: an electron is neither a particle nor a wave but an entity displaying one of both characteristics at different times. So if mathematics really is the underlying formalism for physics, then the QM paradox is `explained' by the Russell paradox which is an example of Gödel's general proof concerning the incompleteness of logical axiomatic systems.

8

This idea probably lies at the heart of any physicists, as simplicity is hoped to be the ultimate expression of reality. In this sense the term `aesthetic' is also often taken to mean `simple'. However, unification not only appeals to scientists. The seventeenths century philosopher Spinoza held the monistic view that all manifestations are based on one ultimate substance, which he sometimes called `God' or `nature'.

9

This idea is also encountered in the last section of appendix A.7. A reference on the idea of creating a universe out of nothing using quantum fluctuations: [#!BT86!#].

10

In note [#!apdsp2!#] it is pointed out that a possible consequence of the premise of a finite nature of reality is that the universe must be closed, identifying 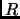$R$ as the radius.