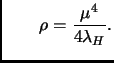 |
(A.2) |
This idea was already encountered in chapter 2 where the notion of field operators developing non-zero expectation values in the vacuum state (VEV) indicated a non-trivial structure of the vacuum. In fact, already the concept of 0-point energy within the context of QM invoked the same picture. In chapter 3 the idea of vacuum energy per se was introduced to explain recent experimental data (this idea of vacuum energy in fact going back to Einstein in the year 1917). Chapter 4 connected the VEV, the vacuum energy and the cosmological constant by virtue of a tachyonic mass parameter
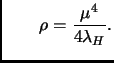 |
(A.2) |